MATEMATICAS

GEOMETRÍA  ANALÍTICA

La geometría analítica estudia las figuras geométricas mediante técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas. Su desarrollo histórico comienza con la geometría cartesiana, impulsada con la aparición de la geometría diferencial de Carl Friedrich Gauss y más tarde con el desarrollo de la geometría algebraica. Actualmente la geometría analítica tiene múltiples aplicaciones más allá de las matemáticas y la ingeniería, pues forma parte ahora del trabajo de administradores para la planeación de estrategias y logística en la toma de decisiones.Las dos cuestiones fundamentales de la geometría analítica son:Dado el lugar geométrico en un sistema de coordenadas, obtener su ecuación.Dada la ecuación en un sistema de coordenadas, determinar la gráfica o lugar geométrico.Lo novedoso de la geometría analítica es que representa las figuras geométricas mediante fórmulas del tipo , donde  es una función u otro tipo de expresión matemática: las rectas se expresan como ecuaciones polinómicas de grado  (por ejemplo, ), las circunferencias y el resto de cónicas como ecuaciones polinómicas de grado 2 (la circunferencia ,la hiprbole  ), etc.

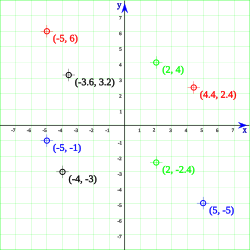
Localización de un punto en el plano cartesiano

Como distancia a los ejes

En un plano traza dos rectas orientadas perpendiculares entre sí (ejes) —que por convenio se trazan de manera que una de ellas sea horizontal y la otra vertical—, y cada punto del plano queda unívocamente determinado por las distancias de dicho punto a cada uno de los ejes, siempre y cuando se dé también un criterio para determinar sobre qué semiplanodeterminado por cada una de las rectas hay que tomar esa distancia, criterio que viene dado por un signo. Ese par de números, las coordenadas quedará representado por un par ordenado , siendo  la distancia a uno de losejes (por convenio será la distancia al eje horizontal) e  la distancia al otro eje (al vertical).En la coordenada, el signo positivo (que suele omitirse) significa que la distancia se toma hacia la derecha sobre el eje horizontal (eje de las abscisas), y el signo negativo (nunca se omite) indica que la distancia se toma hacia la izquierda. Para la coordenada , el signo positivo (también se omite) indica que la distancia se toma hacia arriba sobreel eje vertical (eje de ordenadas), tomándose hacia abajo si el signo es negativo (en ningún caso se omiten los signos negativos).A la coordenada  se la suele denominar abscisa del punto, mientras que a la  se la denomina ordenada del punto.Los puntos del eje de abscisas tienen por lo tanto ordenada igual a , así que serán de la forma , mientras que los del eje de ordenadas tendrán abscisa igual  , por lo que serán de la forma .El punto donde ambos ejes se cruzan tendrá por lo tanto distancia  a cada uno de los ejes, luego su abscisa será  y su ordenada también será . A este punto —el — se le denomina origen de coordenadas.